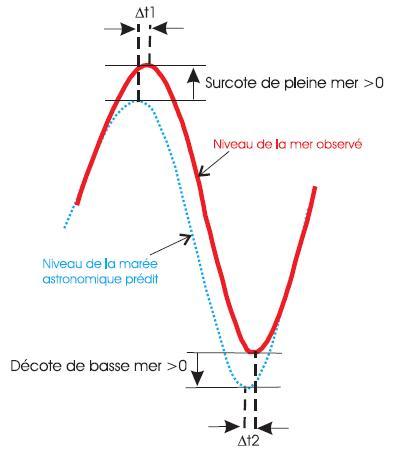
Surcote / décote
La surcote / décote instantanée est la différence, à un instant t, entre la hauteur d'eau observée et la hauteur d'eau prédite. Il s'agit d'une surcote quand cette différence est positive, décote quand elle est négative. La surcote / décote a principalement une origine météorologique : elle est générée, lors du passage de dépressions ou d'anticyclones, par les variations de pression atmosphérique et par les vents. Elle peut avoir également d'autres origines : vagues, seiches, tsunamis…
La surcote de pleine mer est la différence entre la hauteur de pleine mer observée et la hauteur de pleine mer prédite (marée astronomique), les instants d'occurrence de ces deux niveaux pouvant être décalés dans le temps. De même, la décote de basse mer est la différence entre la hauteur de basse mer observée et la hauteur de basse mer prédite.
Niveaux extrêmes
Pour étudier les surcotes/décotes extrêmes (les niveaux extrêmes), les variables appropriées sont la surcote de pleine mer et la décote de basse mer, et non la surcote/décote instantanées. Celles-ci s'affranchissent par définition des effets de déphasage entre l'observation et la prédiction. Ainsi, si seul un déphasage existe entre la hauteur prédite et la hauteur observée, soit pour des raisons physiques, soit parce que les constantes harmoniques sont mal déterminées (par exemple, enregistrement de courte durée ou de mauvaise qualité), les surcotes/décotes instantanées en seront d'autant plus importantes, ce qui n'est pas le cas pour les surcotes de pleine mer et les décotes de basse mer.
Période de retour
Il en résulte que le niveau des plus hautes mers, dont une composante est aléatoire, est une notion qui n'a de sens que si son évaluation s'effectue en terme de probabilité. Il faut chercher l'intervalle moyen de temps, dit période de retour, qui sépare deux évènement rares présentant des niveaux de mer supérieurs à un certain seuil.
Détermination de la période de retour
Exprimé de cette manière, la détermination de la période de retour semble se limiter à un simple calcul de moyenne. Cependant, pour que la moyenne soit significative, il faut disposer de durées d'observations très supérieures aux périodes de retour recherchées. Compte tenu des observations disponibles, on ne pourrait guère estimer des périodes de retour supérieures à deux ou trois ans dans la plupart des cas.
Il est toutefois possible de traiter efficacement ce problème pour les ports, où plus de 10 années d'observations de marée sont disponible, en tirant partit du fait que les surcotes-decotes et la marée sont des phénomène très largement indépendant. En effet, si l'on dispose de nombreuse observation de marée, il peut être aisé de calculer les lois de probabilité régissant des événements rares mais non exceptionnels comme les grandes vives-eaux ou les surcotes très importantes. Mais la simultanéité des deux types d'événement peut n'avoir jamais été observée. Pourtant, la période de retour correspondant à ce type de phénomène rarissime peut se calculer avec un bon degré de confiance en combinant les lois de probabilité liées d'une part à la marée, et d'autre part aux surcotes. Les figures montrent à titre d'exemple, les résultats obtenus pour Brest et présente la probabilité pour une pleine mer prédite d'être égale à une valeur donnée à 1 cm près.
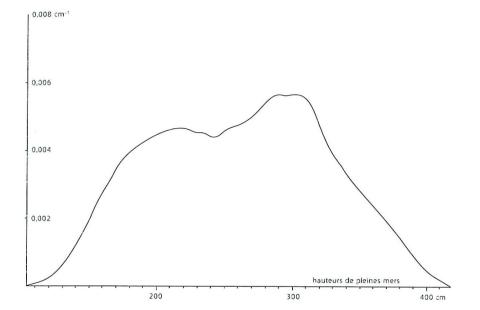
Utilisation de la loi de Gumbel
Le problème qui se pose à propos des surcotes est le calcul de la probabilité associé à une surcote supérieure à une valeur donnée. Une difficulté vient du fait que des surcotes très importantes mais rarissimes ne peuvent pas être ignorées. Des événements qui n'ont jamais été observés doivent être pris en compte à l'aide d'un modèle d'extrapolation. Le modèle choisi est appelé « loi de Gumbel » ; cette loi est utilisée pour l'estimation des crues des fleuves et rivières. L'application de ce modèle à la plus longue série disponible de mesures de hauteur (Brest) a démontré la très bonne adaptation de cette loi pour le niveau marin.
La loi de Gumbel résulte de l'étude des valeurs extrêmes prises par une variable aléatoire au cour de tirages indépendant. L'analyse de ce type de variable ou de celles concernant le dépassement de divers seuils, a été abordée par Fisher et Tuppet et complété par Gumbel. La loi retenue n'est qu'un cas particulier parmi celles qui sont déduite de la théorie des probabilités. Il s'avère qu'elle convient très bien au phénomène des crues ce qui explique son succès.
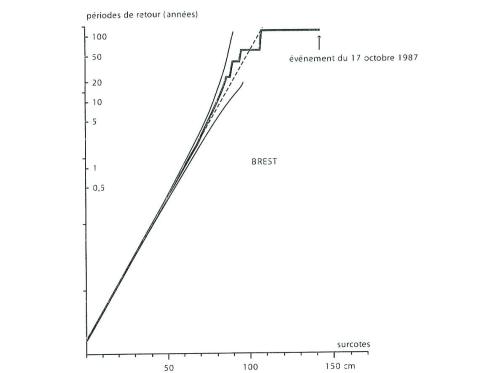
Résultats obtenus
Grâce au traitement séparé de la marée et des surcotes, il s'avère que le choix d'un modèle d'extrapolation n'est pas réellement critique pour l'estimation des périodes de retour des hauteurs extrêmes.
La figure ci-contre présente la probabilité pour qu'une surcote excède une certaine valeur, dans le système de coordonnées défini par Gumbel. Si la loi définie par la relation était respectée, les points expérimentaux, donnant ici un tracé en escalier seraient alignés. La droite en pointillée est celle qui passe au mieux dans le nuage des points expérimentaux. Les deux courbes en trait fin, de part et d'autre de la droite en pointillé, limitent la zone où doivent se situer 90% de points expérimentaux si le modèle d'extrapolation est bien choisi.
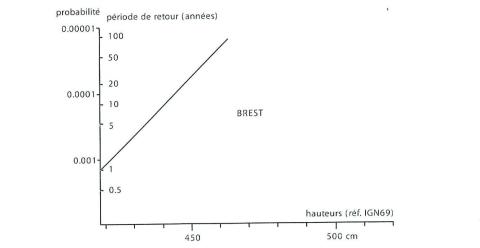
Resultat graphique
La figure est le résultat de la combinaison des lois de probabilité des surcotes et des pleines mers prédites (marée). Le domaine est borné par les valeurs extremums des pleines mers prédites.
Ici la fonction donne les probabilités d'observer des hauteurs de pleines mers supérieures à une valeur donnée, qui peuvent ainsi se traduire en termes de périodes de retour associées. L'exemple ici se focalise uniquement à la présentation des hauteurs supérieures à la hauteur de marée astronomique maximale (les décotes ne sont pas traitées ici).
Cartographie de l'estimation des périodes de retour
L'estimation des périodes de retour peut se calculer, dans certaines conditions, à partir de mesures de hauteur de durée supérieure au mois. Actuellement, les travaux effectués aux points de sondages hydrographiques, à l'aide de capteurs de pression posés sur le fond permettent l'obtention de telles séries de mesure. Il est dès lors possible de tirer profit des relations, existant entre ces mesures et les hauteurs observées simultanément au port de référence le plus proche, afin d'estimer les lois de probabilité nécessaires au calcul des périodes de retour des marées extrêmes en ces points. En raison des caractéristiques de la variabilité spatiale des phénomènes étudiés, il faut s'assurer que la répartition géographique de ces sites présente une densité suffisante pour calculer par interpolation, ces valeurs en tout points de la région étudiée. Dans certaines zones, on dispose ainsi de cartes donnant les lignes d'égales hauteurs de niveau extrêmes.
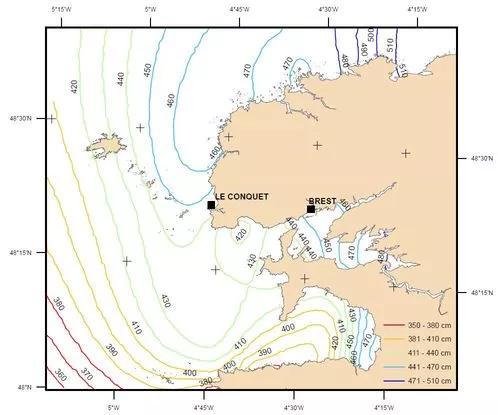
Un exemple de tracé des hauteurs atteintes par la mer pour une période de retour est présenté pour la Mer d'Iroise et la rade de Brest. Cet exemple est le résultat de l'exploitation des données disponibles dans cette zone pour cartographier les niveaux extrêmes correspondant à la période de retour donnée.
Calcul
Le calcul des incertitudes sur les valeurs obtenues est également possible. Les résultats mettent souvent en évidence certaines lacunes du réseau de mesures et permettent de déceler les zones où des observations de marée supplémentaires sont souhaitables.